Những sinh viên theo học ngành trắc địa hoặc các cán bộ đo đạc chắc chắn không còn xa lạ gì với những bài toán cơ bản trong trắc địa. Bài viết dưới đây, Việt Thanh sẽ tổng hợp lại những bài toán thường gặp cũng như cách giải để giúp cho những ai chưa hiểu có thể tra cứu và sử dụng khi cần thiết.
Xem thêm: Ứng dụng máy thủy bình trong đo đạc và tính toán các bài toán cơ bản trong trắc địa.
Bài toán cơ bản trong trắc địa – Bài toán thuận nghịch
Top những bài toán cơ bản trong trắc địa không thể thiếu bài toán liên quan đế thuận nghịch. Cùng tìm hiểu chi tiết và cách giải nhé cùng những ảnh hưởng của nó đến trắc địa nhé.
Bài toán thuận trong trắc địa – Bài toán cơ bản trong trắc địa
Bài toán cơ bản trong trắc địa liên quan đến thuận nghịch là bài toán tính tọa độ vuông góc từ chiều dài và góc định hướng của cạnh. Để xác định được những số liệu này, các cán bộ đo đã sẽ sử dụng đến máy thủy bình hoặc máy toàn đạc điện tử. Những thiết bị thường được sử dụng như như máy toàn đạc Topcon GM-50 Series, máy toàn đạc Sokkia IM-100 Series, máy toàn đạc FX-200 series,…
Bài toán cơ bản như sau:
Giả sử, biết tọa độ điểm A là XA và YB , Chiều dài cạnh giữa hai điểm A, B là SAB và góc định hướng của nó là .Tìm tọa độ điểm B.
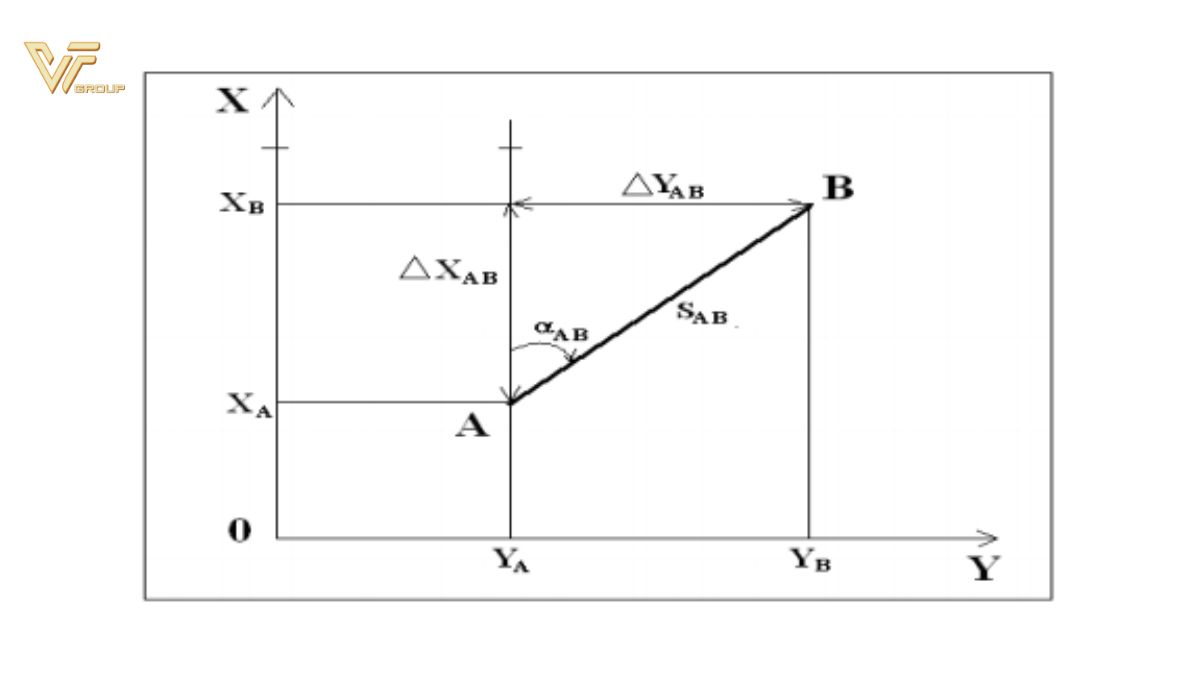
Từ hình trên ta có:
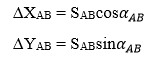
Do đó:
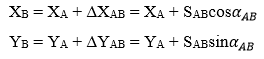
Ví dụ: Cho XA = 2325456,789 (m); YA = 18803234,725 (m); SAB = 1255,463 (m) và góc định hướng của cạnh SAB là 45020’32”2.
Ta tính được: XB = 2325456,789 + 1255,463cos45020’32”2 = 2326339,216 (m)
YB = 18803234,725 + 1255,463sin45020’32”2 = 18804127,759 (m)
Bài toán nghịch – 1 bài toán cơ bản trong trắc địa
Từ hình vẽ trên, nếu biết tọa độ của hai điểm A và B là XA, YA, XB, YB ta có thể tính được chiều dài cạnh SAB và góc định hướng của nó theo công thức:
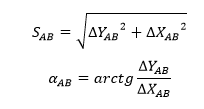
Nội dung của bài toán thuận nghịch trong trắc địa được trình bày ở trên được sử dụng khi xử lý số liệu trong trắc địa.
Xem thêm: Giao hội nghịch – Phương pháp định vị chính xác cho các ứng dụng thực tế
Bài toán cơ bản trong trắc địa – Bài toán về góc định hướng
Nhắc đến các bài toán cơ bản trong trắc địa không thể không nhắc đến bài toán về góc định hướng. Thông thường, để tính toán được góc định hướng, cán bộ đo đạc sẽ sử dụng máy kinh vĩ.
Máy kinh vĩ có thể đo cả góc ngang và góc đứng, giúp xác định chính xác vị trí của các điểm trên mặt đất. Thiết bị này bao gồm một kính ngắm được gắn trên một chân đế có thể xoay, cho phép người đo ngắm vào các điểm khác nhau và đọc các giá trị góc trên các vòng chia độ. Một số sản phẩm máy kinh vĩ được sử dụng như: máy kinh vĩ Satlab SDT2, máy kinh vĩ Nikon NE-100, 101, máy kinh vĩ điện tử Topcon DT-205,..
Bài toán chung về góc định hướng
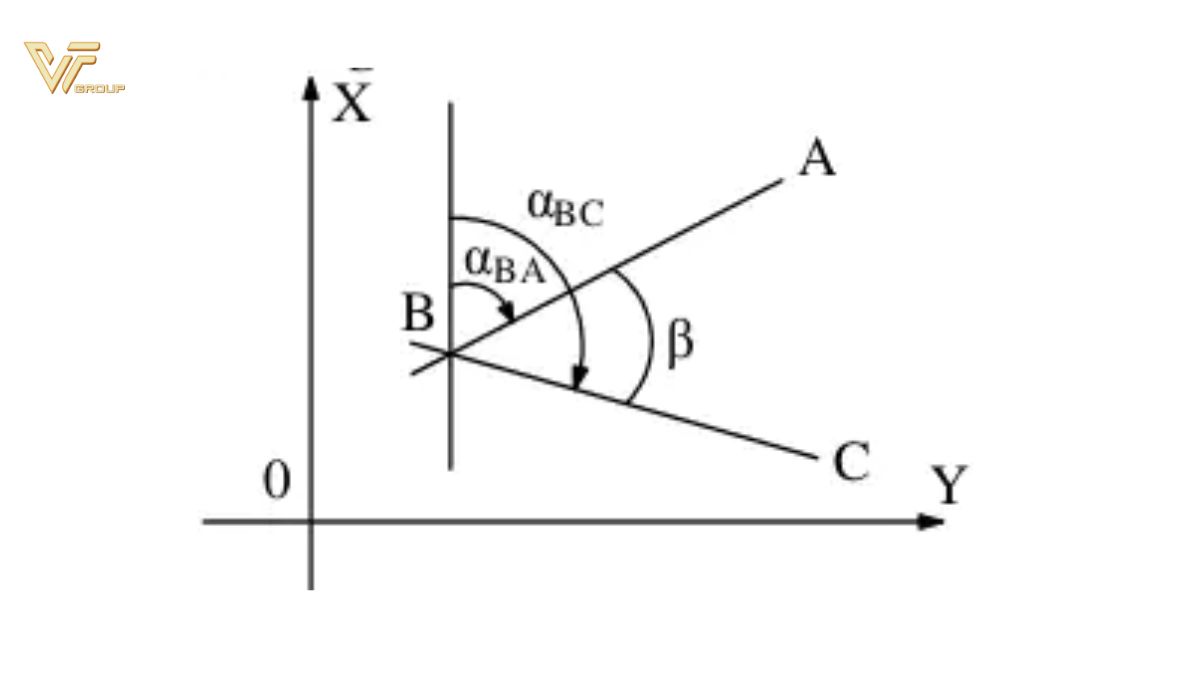
Biết αBA và αBC ta tính được góc β= αBC – αBA
Biết αBA và β ta tính được góc định hướng αBC= αBA + β
Áp dụng 1 bài toán cơ bản trong trắc địa liên quan đến góc định hướng
Trong thực tế đo đạc hiện nay, thông thường ta không thể đo được góc định hướng mà chỉ đo được góc bằng
β. Chính vì vậy, để xác định góc định hướng của một đường thẳng chắc chắn phải dựa vào góc định hướng của một cạnh đã cho trước.
Tính góc định hướng thực của góc β trái
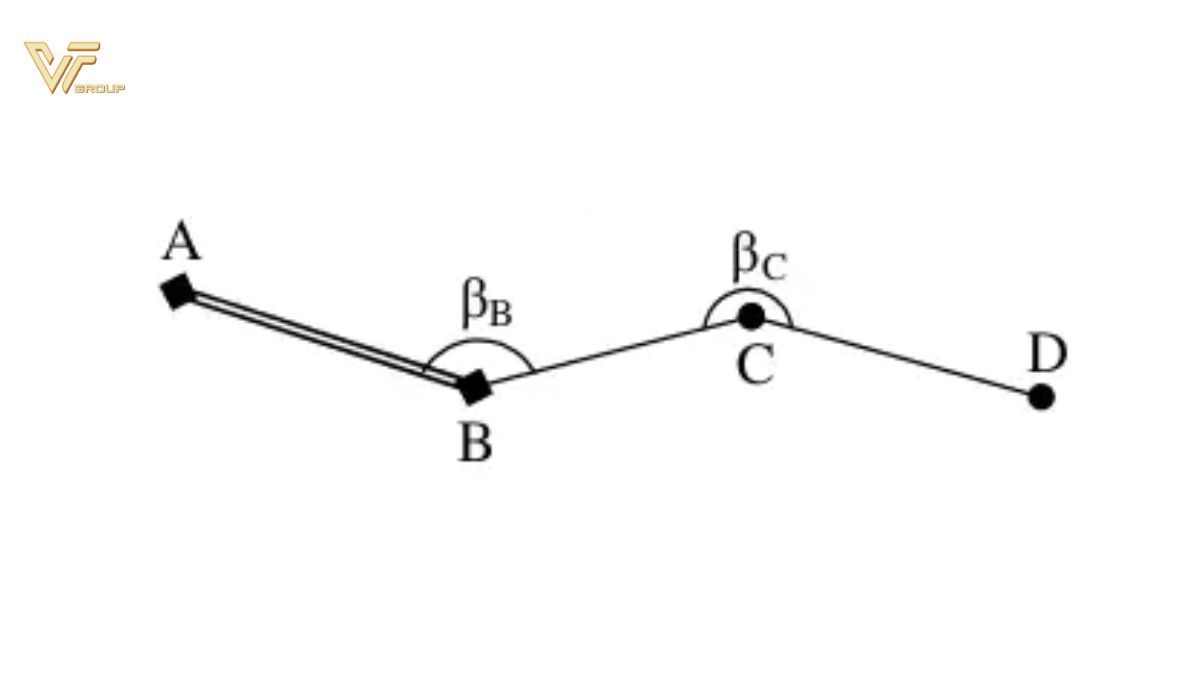
Theo chiều từ A, B, C, D thì các góc βB và βC nằm bên tay phải, khi đó:
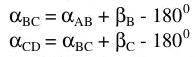
Tính góc định hướng thực của góc β phải
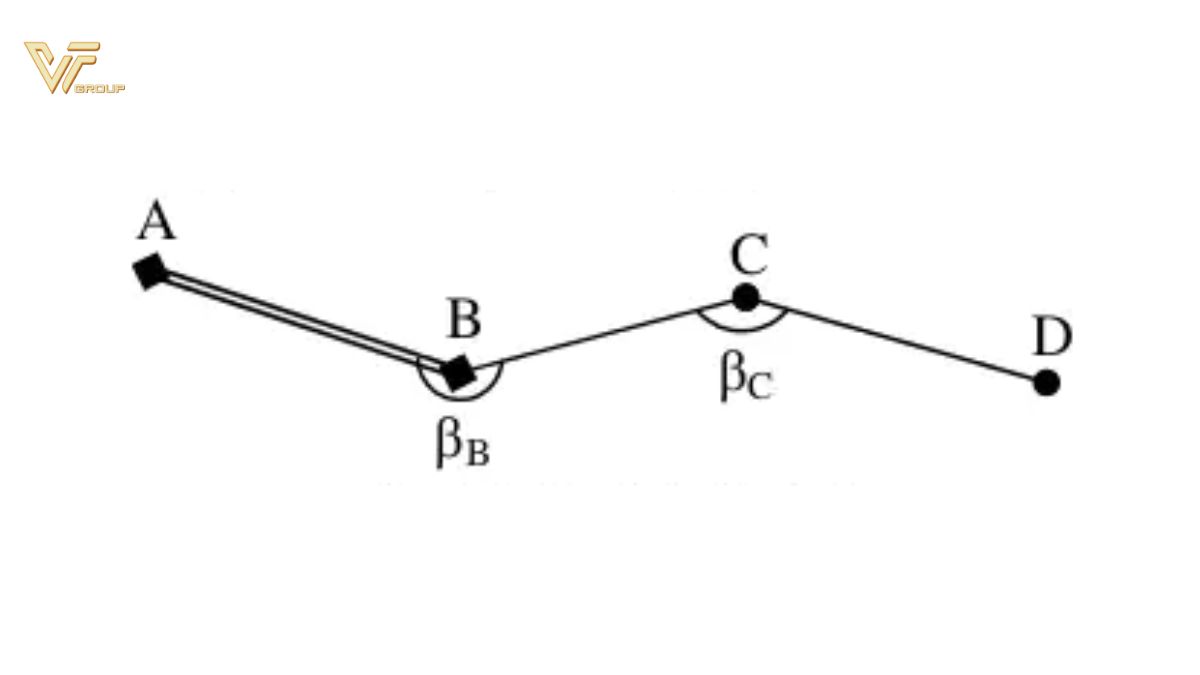
Theo chiều từ A, B, C, D thì các góc βB và βC nằm bên tay phải, khi đó:
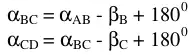
Xem thêm: Góc phương vị là gì? Ứng dụng và cách xác định chi tiết
Bài toán cơ bản trong trắc địa – Bài toán định độ cao
Để chuyển độ cao tuyệt đối (H) của các điểm ta phải biết chênh cao (h) giữa các điểm đó. Có nhiều phương pháp xác định chênh cao nhưng thông dụng nhất là phương pháp đo cao hình học bằng các loại máy thủy bình như máy thủy bình Sokkia B30A; Máy thủy bình Leica NA724; Máy thủy bình Topcon AT-B4A.
Xem thêm: Nguyên lý đo cao độ hình học bằng máy thủy bình
Trong bài toán cơ bản trong trắc địa này để xác định hAB, tại điểm A và B đặt hai cái thước có khắc thành các vạch cm hoặc mm từ 0 đến 3 mét và gọi là mia.
Còn ở giữa đặt một thiết bị đo gọi là máy thủy chuẩn, máy này có khả năng đưa tia ngắm về vị trí nằm ngang (song song với mặt thủy chuẩn tại A) và đọc được chiều cao trên mia trước và mia sau là lT và ls. Từ hình trên ta có:
Trong đó: hAB là chênh cao giữa hai điểm A và B. Nếu ls = 1253mm, lT = 1042mm, ta có h = 211mm
Bằng phương pháp đo chênh cao giữa các điểm i, ta sẽ tính được độ cao Hi các điểm đó bằng cách tính chuyển độ cao tuyệt đối của điểm gốc (H0) đến các điểm đó.
Xem thêm: Phương pháp đo cao hình học: Hướng dẫn chi tiết
Trên đây là tổng hợp những thông tin cơ bản liên quan đến 3 bài toán cơ bản trong trắc địa. Hy vọng những thông tin này sẽ giúp bạn hoàn toàn có thể làm quen với cách giải toán trong ngành trắc địa và ứng dụng vào thực tế. Nếu bạn đọc quan tâm đến các thông tin có liên quan, hãy truy cập website của Việt Thanh để tìm hiểu thêm nhé.
Ngoài ra Việt Thanh còn là đơn vị cung cấp các dịch vụ đo đạc, sửa chữa và hiệu chỉnh thiết bị uy tín hiện nay. Nếu quý khách hàng quan tâm, cần thuê máy thủy bình, máy toàn đạc điện tử, máy GNSS RTK… thì hãy liên hệ hotline 0972.819.598 để được hỗ trợ nhé.
Xem thêm: Phương pháp đo góc đứng: ứng dụng và tầm quan trọng trong trắc địa









Be the first to review “Tổng hợp các bài toán cơ bản trong trắc địa và cách giải chi tiết”