Cơ sở toán học của phương pháp đo ảnh là một trong những kỹ thuật quan trọng trong lĩnh vực trắc địa, giúp xác định vị trí, kích thước và hình dạng của các đối tượng trên bề mặt Trái Đất thông qua việc xử lý ảnh chụp từ không trung hoặc vũ trụ. Hãy cùng Việt Thanh Group tìm hiểu chi tiết về cơ sở toán học của phương pháp đo ảnh, đồng thời khám phá cách ứng dụng phương pháp này trong trắc địa để giải quyết các bài toán thực tế nhé.
>>> Xem thêm: Công cụ giúp đo đạc hiện đại là máy GNSS RTK, máy thuỷ bình đảm bảo hiệu quả và chính xác để thực hiện các dự án lớn nhỏ.
Tìm hiểu cơ sở toán học của phương pháp đo ảnh là gì?
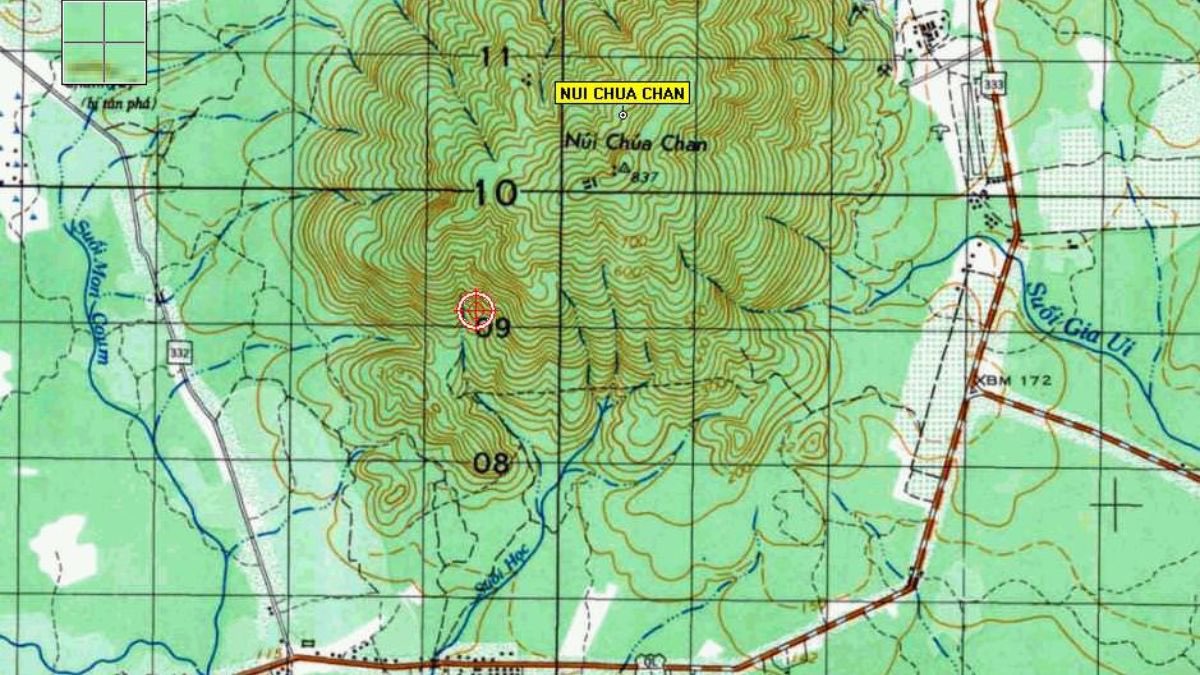
Cơ sở toán học của phương pháp đo ảnh là nền tảng lý thuyết và các nguyên tắc toán học giúp chuyển đổi thông tin từ ảnh chụp hai chiều (2D) thành thông tin không gian ba chiều (3D). Các phương pháp này dựa trên các nguyên lý hình học, như phép chiếu trung tâm, phép chiếu bản đồ, và phương pháp điều chỉnh số liệu, để tính toán chính xác vị trí, kích thước, và khoảng cách của các đối tượng trên bề mặt Trái Đất thông qua ảnh chụp từ các thiết bị như camera, máy bay, hoặc vệ tinh.
Trong phương pháp đo ảnh, các công thức toán học giúp xác định tọa độ không gian (X, Y, Z) của các điểm trong thế giới thực dựa trên tọa độ của chúng trên ảnh (X’, Y’). Các nguyên lý này đảm bảo rằng thông tin thu thập được từ ảnh có độ chính xác cao và có thể sử dụng trong các ứng dụng như lập bản đồ, khảo sát địa hình, và quản lý tài nguyên.
>>> Xem thêm: Các dự án bàn giao thiết bị đo đạc thành công tại Việt Thanh Group.
Những cơ sở toán học của phương pháp đo ảnh
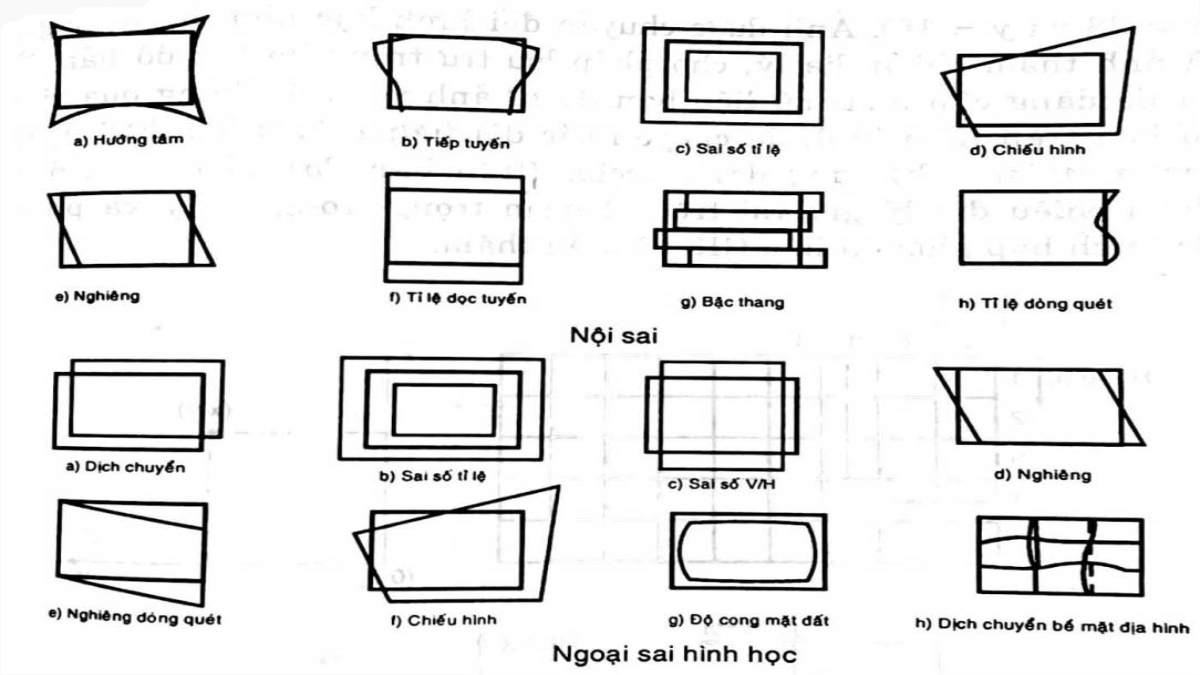
Dưới đây là những cơ sở toán học chính của phương pháp này:
Hình học chiếu trong phương pháp đo ảnh
Một trong những nền tảng toán học quan trọng của phương pháp đo ảnh là hình học chiếu. Khi một điểm trong không gian ba chiều được chiếu lên mặt phẳng hình ảnh, tọa độ của nó bị thay đổi theo quy luật của phép chiếu phối cảnh. Trong phép chiếu này, các điểm không gian được kết nối với tâm chiếu (vị trí của máy ảnh), sau đó được phản chiếu lên mặt phẳng 2D của bức ảnh.
Công thức chiếu phối cảnh cơ bản:
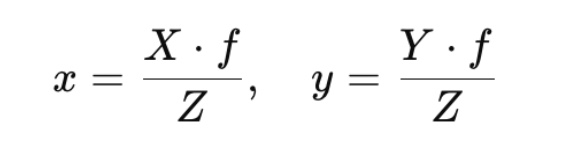
Trong đó:
- X,Y,Z là tọa độ thực tế của điểm trong không gian ba chiều.
- x,y là tọa độ điểm trên mặt phẳng ảnh.
- f là tiêu cự của máy ảnh.
Phép chiếu này cho phép chuyển đổi thông tin từ không gian 3D sang hình ảnh 2D, từ đó ta có thể sử dụng các phương pháp toán học khác để tái tạo lại tọa độ ban đầu.
Phương pháp lập thể trong đo ảnh
Phương pháp lập thể (stereophotogrammetry) là kỹ thuật sử dụng hai hoặc nhiều ảnh từ các góc chụp khác nhau để tái tạo mô hình 3D. Toán học của lập thể dựa trên việc tìm giao điểm của các tia chiếu từ nhiều máy ảnh đến các điểm trên ảnh. Thông qua công thức tam giác cơ sở, ta có thể xác định khoảng cách và vị trí của các điểm trong không gian.
Công thức tam giác cơ sở:
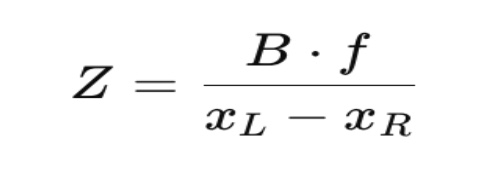
Trong đó:
- B là khoảng cách giữa hai máy ảnh (baseline).
- f là tiêu cự của máy ảnh.
- xL và xR là tọa độ của điểm trên hai ảnh trái và phải.
Sự chính xác của phương pháp này phụ thuộc vào độ chính xác trong việc đo đạc khoảng cách giữa các máy ảnh và tọa độ điểm ảnh.
Lý thuyết đồng dạng và tỷ lệ trong đo ảnh
Lý thuyết đồng dạng là một phần quan trọng trong việc xác định tỷ lệ giữa các kích thước trên ảnh và kích thước thực tế. Hai tam giác đồng dạng sẽ có các cạnh tương ứng tỷ lệ thuận với nhau, điều này cho phép ta tính toán kích thước thực tế từ những phép đo trên ảnh.
Công thức đồng dạng:
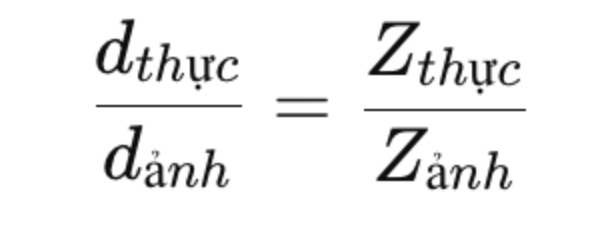
Trong đó:
- dthực là kích thước thực tế của đối tượng.
- dảnh là kích thước của đối tượng trên ảnh.
- Zthực và Zảnh là khoảng cách từ máy ảnh đến đối tượng thực tế và trên ảnh.
Việc sử dụng lý thuyết đồng dạng giúp xác định chính xác tỷ lệ và kích thước của các đối tượng trong không gian 3D từ hình ảnh 2D.
Phép chiếu đồng thời và bình sai trong đo ảnh
Khi có nhiều hình ảnh hoặc dữ liệu đo đạc từ các nguồn khác nhau, phương pháp bình sai (least squares adjustment) được áp dụng để tối ưu hóa kết quả. Bình sai cho phép điều chỉnh các kết quả đo đạc để giảm thiểu sai số và đưa ra giá trị chính xác nhất cho tọa độ của các điểm đo.
Phương pháp này đặc biệt hữu ích trong các dự án lớn, nơi dữ liệu được thu thập từ nhiều góc độ và thiết bị khác nhau. Bằng cách tối ưu hóa thông qua các phương trình tuyến tính và phi tuyến, ta có thể giảm thiểu độ lệch và cải thiện độ chính xác của mô hình 3D thu được.
Chuyển đổi hệ tọa độ trong đo ảnh
Chuyển đổi tọa độ là một yếu tố quan trọng trong đo ảnh, đặc biệt khi cần liên kết tọa độ của các điểm trên ảnh với tọa độ thực tế trong không gian ba chiều. Các phép biến đổi affine và phép quay giúp thay đổi hệ tọa độ từ không gian ảnh sang không gian thực, giúp ta xác định đúng vị trí của các đối tượng.
Một ví dụ điển hình của chuyển đổi tọa độ là việc sử dụng hệ tọa độ địa phương và hệ tọa độ toàn cầu trong các dự án bản đồ. Qua đó, các dữ liệu hình ảnh có thể được tích hợp và sử dụng trong các hệ thống thông tin địa lý (GIS).
>>> Xem thêm: Máy Thủy Bình Sokkia , Máy Thủy Bình Leica , Máy Thủy Bình Hi-Target giúp nâng cao chất lượng công việc trong các lĩnh vực đo đạc địa lý và các máy thủy bình nổi bật như:Máy Thủy Bình Hi-Target HT32, Máy Thủy Bình Sokkia B40A, Máy Thủy Bình Nikon AX-2S
Ứng dụng cơ sở toán học của phương pháp đo ảnh trong trắc địa

Lập bản đồ địa hình
Phương pháp đo ảnh là công cụ quan trọng trong việc lập bản đồ địa hình. Nhờ cơ sở toán học mạnh mẽ, kỹ thuật này giúp xác định chính xác độ cao, khoảng cách và hình dạng của các đối tượng địa lý. Các mô hình 3D từ ảnh chụp không trung thường được sử dụng để tạo ra các bản đồ địa hình chi tiết, phục vụ cho các dự án xây dựng, quy hoạch và quản lý đất đai.
Khảo sát công trình xây dựng
Trong xây dựng, phương pháp đo ảnh được sử dụng để khảo sát các công trình từ trên cao, giúp các kỹ sư và nhà quản lý có cái nhìn tổng quan về địa hình và môi trường xung quanh. Phương pháp này cũng hỗ trợ trong việc đo đạc chính xác các khoảng cách và kích thước của các đối tượng xây dựng.
Quản lý tài nguyên thiên nhiên
Phương pháp đo ảnh cũng được ứng dụng trong quản lý tài nguyên thiên nhiên, từ việc theo dõi sự thay đổi của môi trường, rừng và đất đai đến việc đo đạc và quản lý các công trình hạ tầng. Các ảnh chụp từ vệ tinh và máy bay cung cấp thông tin giá trị về các thay đổi môi trường, giúp các nhà khoa học và quản lý đưa ra các quyết định chính xác về bảo vệ tài nguyên.
>>> Xem thêm: Đo lưới khống chế mặt bằng GPS: Tìm hiểu chi tiết
Lợi ích cơ sở toán học của phương pháp đo ảnh
- Tính chính xác cao: Với cơ sở toán học vững chắc, phương pháp đo ảnh mang lại độ chính xác cao trong việc xác định các đối tượng và thông tin không gian. Điều này đặc biệt quan trọng trong trắc địa, nơi mỗi sai số nhỏ có thể dẫn đến hậu quả lớn trong xây dựng và quy hoạch.
- Tiết kiệm thời gian và chi phí: So với các phương pháp đo đạc truyền thống, phương pháp đo ảnh giúp tiết kiệm thời gian và chi phí đáng kể. Các thiết bị hiện đại như drone, vệ tinh có thể thu thập thông tin trên diện rộng mà không cần nhiều nhân lực.
- Ứng dụng đa dạng: Phương pháp này không chỉ hữu ích trong trắc địa mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác như quản lý tài nguyên, môi trường, nông nghiệp chính xác và giám sát thiên tai.
>>> Xem thêm: Phương pháp giao hội góc: Cách xác định vị trí chính xác trong trắc địa
Cơ sở toán học của phương pháp đo ảnh đóng vai trò quan trọng trong việc đảm bảo tính chính xác và hiệu quả của quá trình đo đạc và phân tích dữ liệu không gian. Với sự phát triển của công nghệ, phương pháp này ngày càng trở nên phổ biến và hữu dụng trong trắc địa cũng như nhiều lĩnh vực khác. Việt Thanh Group tự hào là đơn vị hàng đầu trong việc cung cấp các dịch vụ cho thuê thiết bị đo đạc với đội ngũ nhân viên hỗ trợ chuyên nghiệp trên toàn quốc.









Be the first to review “Cơ sở toán học của phương pháp đo ảnh: Hiểu rõ nguyên lý và ứng dụng trong trắc địa”