Trong nhiều lĩnh vực như địa lý, kỹ thuật xây dựng, và khoa học máy tính, việc tính toán khoảng cách giữa hai điểm tọa độ là một kỹ năng quan trọng. Hiểu rõ và sử dụng thành thạo công thức này sẽ giúp bạn thực hiện các công việc chính xác và hiệu quả hơn. Có thể sử dụng máy GPS RTK để hỗ trợ công tác tính khoảng cách tốt nhất. Hãy cùng Việt Thanh Group tìm hiểu về các công thức tính khoảng cách giữa 2 điểm tọa độ.
Công thức tính khoảng cách giữa 2 điểm tọa độ
Khoảng cách giữa hai điểm tọa độ là một khái niệm quan trọng và phổ biến trong nhiều lĩnh vực khoa học và kỹ thuật. Dù bạn đang làm việc trong lĩnh vực địa lý, lập trình, hay xây dựng, việc hiểu và áp dụng đúng các công thức tính khoảng cách giữa hai điểm sẽ giúp công việc của bạn trở nên chính xác và hiệu quả hơn. Dưới đây là công thức tính khoảng cách:
Có thể sử dụng máy GPS RTK, máy toàn đạc điện tử đang được cung cấp ở Việt Thanh Group để hỗ trợ công tác tính khoảng cách. Một số thương hiệu nổi bật của máy GPS RTK như máy GNSS RTK Hi-Target, máy GNSS RTK Satlab….Trong đó, model như Hi-Target 500, Satlab Freyja đo đạc tốt, kết quả chính xác.
Công thức Euclid (trong không gian 2 chiều)
Công thức Euclid là một trong những công thức cơ bản và phổ biến nhất để tính khoảng cách giữa hai điểm trong không gian 2 chiều. Giả sử chúng ta có hai điểm A(x1, y1) và B(x2, y2). Khoảng cách giữa hai điểm này được tính bằng công thức:
D = sqrt((x2 – x1)^2 + (y2 – y1)^2)
Trong đó:
- D là khoảng cách giữa hai điểm A và B.
- (x1, y1) là tọa độ của điểm A.
- (x2, y2) là tọa độ của điểm B.
Công thức này dựa trên định lý Pythagoras, áp dụng cho tam giác vuông được hình thành bởi đoạn thẳng nối hai điểm và các đoạn thẳng song song với các trục tọa độ.
Công thức Euclid (trong không gian 3 chiều)
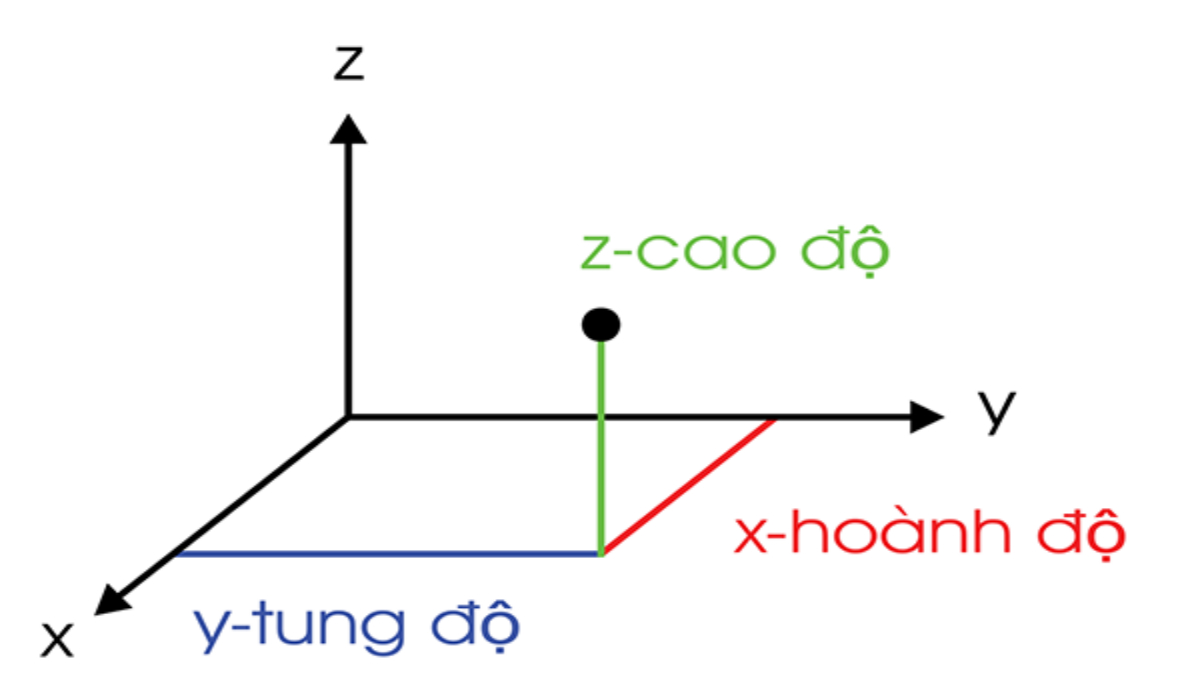
Nếu hai điểm nằm trong không gian 3 chiều, công thức Euclid được mở rộng để tính khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2, z2) như sau:
D = sqrt((x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2)
Trong đó:
- D là khoảng cách giữa hai điểm A và B.
- (x1, y1, z1) là tọa độ của điểm A.
- (x2, y2, z2) là tọa độ của điểm B.
Công thức này tương tự như công thức trong không gian 2 chiều, nhưng có thêm thành phần khoảng cách theo trục z để tính toán khoảng cách trong không gian 3 chiều.
Công thức Haversine (trên bề mặt trái đất)
Khi tính khoảng cách giữa hai điểm tọa độ trên bề mặt Trái Đất, chúng ta cần sử dụng công thức Haversine để tính khoảng cách cung tròn lớn giữa hai điểm có tọa độ kinh độ và vĩ độ. Giả sử điểm A có tọa độ (lat1, lon1) và điểm B có tọa độ (lat2, lon2), công thức Haversine được viết như sau:
a = sin^2((lat2 – lat1) / 2) + cos(lat1) * cos(lat2) * sin^2((lon2 – lon1) / 2)
c = 2 * atan2(sqrt(a), sqrt(1 – a))
D = R * c
Trong đó:
- lat1, lon1 là tọa độ vĩ độ và kinh độ của điểm A (tính bằng radian).
- lat2, lon2 là tọa độ vĩ độ và kinh độ của điểm B (tính bằng radian).
- R là bán kính của Trái Đất (khoảng 6,371 km).
- a và c là các biến trung gian được sử dụng để tính khoảng cách D.
Công thức Haversine rất hữu ích trong các ứng dụng liên quan đến bản đồ và GPS, giúp tính toán khoảng cách giữa hai điểm trên bề mặt cong của Trái Đất.
>>>Xem thêm: Thẩm quyền trích đo địa chính thửa đất thuộc về cơ quan nào
Ứng dụng thực tế của công thức tính khoảng cách
Ứng dụng trong hệ thống định vị GPS
Công thức Haversine được sử dụng rộng rãi trong hệ thống định vị GPS để tính toán khoảng cách giữa hai điểm trên bề mặt Trái Đất. Điều này rất hữu ích cho các ứng dụng bản đồ, dẫn đường và theo dõi vị trí. Chẳng hạn, khi bạn sử dụng ứng dụng bản đồ trên điện thoại để tìm đường, ứng dụng sẽ sử dụng công thức này để tính khoảng cách và hướng đi.
Ứng dụng trong địa lý và địa chất
Trong nghiên cứu địa lý và địa chất, việc tính toán khoảng cách giữa hai điểm tọa độ giúp các nhà khoa học đo đạc và phân tích các hiện tượng tự nhiên, địa hình và cấu trúc địa chất. Ví dụ, khoảng cách giữa hai điểm quan trắc trên một ngọn núi có thể giúp xác định sự di chuyển của các mảng đất.
Ứng dụng trong kỹ thuật xây dựng
Các kỹ sư xây dựng sử dụng công thức tính khoảng cách để thiết kế và thi công các công trình xây dựng, đảm bảo tính chính xác và an toàn của các dự án. Việc tính toán khoảng cách giữa các điểm trong bản vẽ xây dựng giúp xác định vị trí và kích thước của các cấu trúc một cách chính xác.
Ứng dụng trong khoa học máy tính
Trong khoa học máy tính, việc tính toán khoảng cách giữa hai điểm tọa độ được sử dụng trong các thuật toán tìm kiếm, phân loại và học máy. Chẳng hạn, trong các thuật toán máy học như K-Nearest Neighbors (KNN), khoảng cách giữa các điểm dữ liệu được sử dụng để phân loại hoặc dự đoán.
Ngoài ra, Việt Thanh Group có dịch vụ cho thuê thiết bị đo đạc uy tín.
>>>Xem thêm: Lưới đường chuyền hạng 4 là gì
Việc nắm vững và sử dụng thành thạo các công thức tính khoảng cách giữa hai điểm tọa độ không chỉ giúp bạn thực hiện các công việc chính xác hơn mà còn mở rộng khả năng ứng dụng của bạn trong nhiều lĩnh vực khác nhau. Từ công thức Euclid trong không gian 2 chiều và 3 chiều đến công thức Haversine trên bề mặt Trái Đất, mỗi công thức đều có vai trò quan trọng và ứng dụng rộng rãi trong thực tiễn. Mọi người muốn tìm hiểu thông tin cách tính khoảng cách giữa 2 điểm tọa độ thì có thể truy cập Công ty Cổ phần Tập đoàn Việt Thanh.









Be the first to review “Hướng dẫn chi tiết công thức tính khoảng cách giữa 2 điểm tọa độ”